Introducción al machine learning#
Aprendizaje supervisado#
¡Bienvenido/a al primer paso en tu aprendizaje de machine learning! Este notebook se centra en los fundamentos del aprendizaje supervisado, una de las ramas más utilizadas en Machine Learning, donde el modelo aprende a partir de datos etiquetados para hacer predicciones o clasificaciones.
##¿Qué es el aprendizaje supervisado? El aprendizaje supervisado es un enfoque en el que un modelo se entrena utilizando un conjunto de datos en el que cada muestra tiene una etiqueta o resultado conocido. El objetivo es que el modelo sea capaz de predecir esta etiqueta en nuevas muestras de datos desconocidos. Imagina que tienes un conjunto de datos de condiciones meteorológicas (como la temperatura y la humedad) y deseas que el modelo prediga si lloverá o no. Con el aprendizaje supervisado, puedes enseñarle al modelo a reconocer patrones en los datos para responder esta pregunta.
##Aplicaciones del aprendizaje supervisado Existen múltiples aplicaciones del aprendizaje supervisado en la vida diaria y en diversas industrias, como:
Medicina: Diagnosticar enfermedades a partir de síntomas o análisis de imágenes médicas.
Finanzas: Evaluar el riesgo crediticio de una persona basado en su historial.
Meteorología: Predecir condiciones climáticas, como la probabilidad de lluvia o temperatura en un día específico.
Marketing: Clasificar a los clientes en diferentes categorías para diseñar estrategias personalizadas.
##Objetivo del notebook En este notebook, abordaremos dos de las técnicas más comunes en el aprendizaje supervisado:
Regresión lineal: Útil para predecir valores continuos, como el precio de una casa según su tamaño o la temperatura en función de la humedad.
Clasificación binaria: Útil para categorizar datos en dos clases, como «lloverá» o «no lloverá» según las condiciones atmosféricas.
#Sección 1: Regresión lineal La regresión lineal es una técnica de machine learning supervisado que se utiliza para predecir un valor continuo en función de una o más variables. En su forma más simple, la regresión lineal encuentra la relación entre dos variables y traza una línea que mejor representa esa relación.
La ecuación general de una regresión lineal simple es:
donde:
𝑦 es el valor que queremos predecir,
𝑥 es la variable independiente o predictor,
𝑚 es la pendiente de la línea (indica la relación entre 𝑥 e 𝑦),
𝑏 es la intersección o el punto donde la línea cruza el eje 𝑦.
###¿Cuándo utilizar la regresión lineal? La regresión lineal es adecuada cuando creemos que hay una relación lineal entre la variable independiente y la dependiente. Algunos ejemplos típicos son:
Predicción de precios: como el precio de una casa basado en su tamaño,
Predicción de temperaturas: como la temperatura según la hora del día o el nivel de humedad,
Modelos de ventas: como el número de productos vendidos en función del tiempo o la cantidad de inversión en marketing.
###Ejemplo práctico: Predicción de temperatura en función de la humedad Supongamos que tenemos datos históricos sobre la temperatura y la humedad en un área determinada, y queremos modelar cómo la temperatura depende de la humedad.
Primero, vamos a generar algunos datos de ejemplo y realizar la regresión lineal utilizando scikit-learn, una de las librerías más comunes para machine learning en Python. Al mismo tiempo, explicaremos los conceptos clave para que entiendas qué sucede en cada paso.
##Código y explicación paso a paso Primero, si no tienes instalada la librería scikit-learn, debes instalarla ejecutando el siguiente comando:
!pip install -U scikit-learn
Ahora, veamos el código para este ejemplo de regresión lineal.
# importamos las librerías necesarias
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression # importamos el modelo de regresión lineal
# generamos datos de ejemplo (en un caso real, tendríamos datos históricos reales)
np.random.seed(0) # fija una semilla para reproducibilidad
humedad = np.random.rand(100, 1) * 100 # generamos 100 puntos de humedad entre 0 y 100
temperatura = 0.5 * humedad + np.random.randn(100, 1) * 5 + 10 # simulamos temperaturas con un poco de ruido
# instanciamos el modelo de regresión lineal
modelo = LinearRegression()
# ajustamos el modelo a los datos
modelo.fit(humedad, temperatura)
# realizamos predicciones con los datos
temperatura_pred = modelo.predict(humedad)
# graficamos los datos y la línea de regresión
plt.scatter(humedad, temperatura, color='blue', label='datos reales')
plt.plot(humedad, temperatura_pred, color='red', label='línea de regresión')
plt.xlabel('humedad (%)')
plt.ylabel('temperatura (°C)')
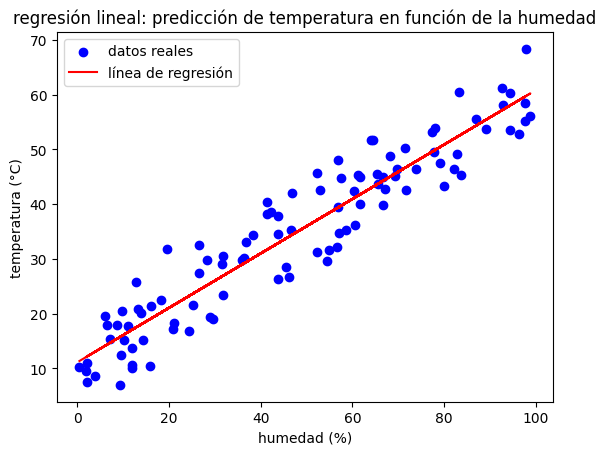
plt.title('regresión lineal: predicción de temperatura en función de la humedad')
plt.legend()
plt.show()
##Explicación detallada del código ###Importación de librerías:
numpy es para manejar matrices y operaciones numéricas.
matplotlib.pyplot permite graficar.
sklearn.linear_model.LinearRegression es la clase de regresión lineal de scikit-learn.
###Generación de datos:
np.random.rand(100, 1) * 100 genera 100 valores de humedad entre 0 y 100.
temperatura = 0.5 * humedad + np.random.randn(100, 1) * 5 + 10 simula valores de temperatura con una relación lineal aproximada respecto a la humedad y agrega un poco de ruido aleatorio con np.random.randn(100, 1) * 5 para hacerlo más realista.
###Instanciación del modelo:
modelo = LinearRegression() crea una instancia del modelo de regresión lineal.
ajuste del modelo:
modelo.fit(humedad, temperatura) utiliza los datos de humedad y temperatura para ajustar el modelo. Este paso calcula la pendiente y el intercepto óptimos de la línea de regresión.
###Predicción:
temperatura_pred = modelo.predict(humedad) calcula la temperatura predicha por el modelo para cada valor de humedad en los datos originales.
graficación:
plt.scatter(humedad, temperatura, color='blue', label='datos reales') grafica los datos originales en azul.
plt.plot(humedad, temperatura_pred, color='red', label='línea de regresión') grafica la línea de regresión en rojo para mostrar la relación lineal.
Los comandos plt.xlabel, plt.ylabel, y plt.title etiquetan los ejes y el título, mientras plt.legend() muestra la leyenda.
###Interpretación de los resultados
En el gráfico, los puntos azules representan los datos originales, mientras que la línea roja es la línea de regresión obtenida. La pendiente y el intercepto de esta línea son los que mejor ajustan los datos en términos de minimizar la distancia entre los puntos y la línea de predicción.
Este modelo nos permite realizar predicciones de temperatura basadas en los valores de humedad que observamos. Si quisiéramos predecir la temperatura en un día con 70% de humedad, solo necesitaríamos ingresar este valor en el modelo ajustado, que nos devolverá una temperatura estimada.
#Sección 2: clasificación binaria
En esta sección, exploraremos el concepto de clasificación binaria, que es uno de los tipos de problemas de aprendizaje supervisado más comunes. En una tarea de clasificación binaria, el objetivo es asignar una observación a una de dos clases posibles, basándonos en sus características. Este tipo de problema aparece frecuentemente en aplicaciones como:
Clasificación de correos electrónicos (spam o no spam)
Diagnóstico médico (enfermedad presente o ausente)
Predicción de eventos (lloverá o no lloverá)
##¿Qué es la clasificación binaria?
La clasificación binaria implica tomar decisiones sobre datos que tienen solo dos posibles categorías de salida. Para esto, un modelo aprende a clasificar las observaciones en una de las dos clases usando un conjunto de datos con etiquetas predefinidas.
##¿Cómo funciona?
Definición de clases: Primero, definimos nuestras dos clases, como «lloverá» y «no lloverá».
Entrenamiento: Entrenamos el modelo con datos etiquetados, como humedad, temperatura y si llovió o no.
Predicción: El modelo utiliza el conocimiento aprendido para clasificar datos nuevos en una de las dos clases.
##Ejemplo práctico Predecir si lloverá según datos meteorológicos. Imaginemos que queremos predecir si va a llover (1) o no va a llover (0) basándonos en la temperatura y la humedad relativa. A continuación, mostramos cómo entrenar un clasificador binario simple usando la regresión logística.
###Fórmula de la regresión logística La regresión logística es un método popular para la clasificación binaria, y su fórmula matemática se basa en la función sigmoide:
donde:
\( \beta_0 \) es el intercepto.
\( \beta_1, \beta_2, \dots, \beta_n \) son los coeficientes asociados a cada predictor \( X_1, X_2, \dots, X_n \).
\( P(Y = 1|X) \) es la probabilidad de que la clase sea 1 (lloverá) dado el valor de \( X \).
A continuación, implementamos el ejemplo en código:
##Implementación en código
# Importamos las bibliotecas necesarias
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
# Generamos un conjunto de datos ampliado
data = {
'Temperatura (°C)': [18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 18, 19, 21, 23, 25, 27, 29, 31, 33, 35,
19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40],
'Humedad (%)': [65, 70, 75, 80, 85, 90, 60, 55, 50, 45, 66, 71, 76, 81, 86, 91, 61, 56, 51, 46,
68, 73, 78, 83, 88, 93, 63, 58, 53, 48, 67, 72, 77, 82, 87, 92, 62, 57, 52, 47],
'Lluvia': [1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0]
}
# Convertimos los datos a un DataFrame
df = pd.DataFrame(data)
# Definimos las variables de entrada (X) y de salida (y)
X = df[['Temperatura (°C)', 'Humedad (%)']]
y = df['Lluvia']
# Dividimos los datos en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Creamos y entrenamos el modelo de regresión logística
modelo = LogisticRegression()
modelo.fit(X_train, y_train)
# Hacemos predicciones en el conjunto de prueba
y_pred = modelo.predict(X_test)
# Evaluamos el modelo
precision = accuracy_score(y_test, y_pred)
matriz_confusion = confusion_matrix(y_test, y_pred)
print("Precisión del modelo:", precision)
print("Matriz de confusión:")
print(matriz_confusion)
# Visualización de las predicciones
plt.figure(figsize=(8, 6))
sns.scatterplot(data=df, x='Temperatura (°C)', y='Humedad (%)', hue='Lluvia', palette='coolwarm', edgecolor='k', s=100)
plt.title('Predicción de Lluvia: 0 = No llueve, 1 = Llueve')
plt.xlabel('Temperatura (°C)')
plt.ylabel('Humedad (%)')
plt.legend(title='Clase')
plt.show()
Precisión del modelo: 1.0
Matriz de confusión:
[[8 0]
[0 4]]
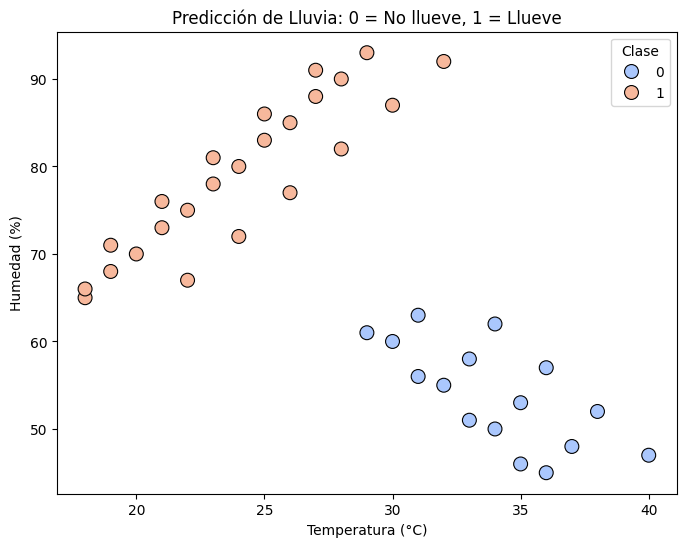
###Explicación del código
Generación de datos de ejemplo: Creamos datos de temperatura y humedad aleatorios y etiquetamos las observaciones en función de una relación lineal aproximada.
División de datos: Utilizamos train_test_split para dividir los datos en conjuntos de entrenamiento y prueba.
Creación del modelo: Creamos un modelo de regresión logística usando LogisticRegression.
Entrenamiento: Entrenamos el modelo en el conjunto de entrenamiento.
Predicción y evaluación: Realizamos predicciones en el conjunto de prueba, evaluamos la precisión y mostramos la matriz de confusión.
Visualización: Graficamos los resultados con una visualización de puntos de colores para identificar las predicciones del modelo.
#Sección 3: Ejemplos ##Ejemplo 1: Predicción de precios de viviendas (Regresión Lineal) Queremos predecir el precio de una vivienda basándonos en su tamaño (metros cuadrados). Este ejemplo ilustra una relación directa entre una variable independiente (el tamaño) y una dependiente (el precio).
# Importamos las bibliotecas necesarias
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Generamos un conjunto de datos
data = {
'Tamaño (m2)': [50, 80, 120, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700, 750, 800, 850, 900, 950],
'Precio (USD)': [150000, 200000, 280000, 340000, 450000, 540000, 620000, 700000, 780000, 860000,
940000, 1020000, 1100000, 1180000, 1260000, 1340000, 1420000, 1500000, 1580000, 1660000]
}
df = pd.DataFrame(data)
# Definimos las variables de entrada (X) y de salida (y)
X = df[['Tamaño (m2)']]
y = df['Precio (USD)']
# Dividimos los datos en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Creamos y entrenamos el modelo de regresión lineal
modelo = LinearRegression()
modelo.fit(X_train, y_train)
# Hacemos predicciones en el conjunto de prueba
y_pred = modelo.predict(X_test)
# Calculamos el error cuadrático medio (MSE)
mse = mean_squared_error(y_test, y_pred)
print("Error cuadrático medio (MSE):", mse)
# Visualización de la regresión
import matplotlib.pyplot as plt
plt.scatter(X, y, color='blue', label='Datos reales')
plt.plot(X_test, y_pred, color='red', label='Predicción')
plt.xlabel('Tamaño (m2)')
plt.ylabel('Precio (USD)')
plt.legend()
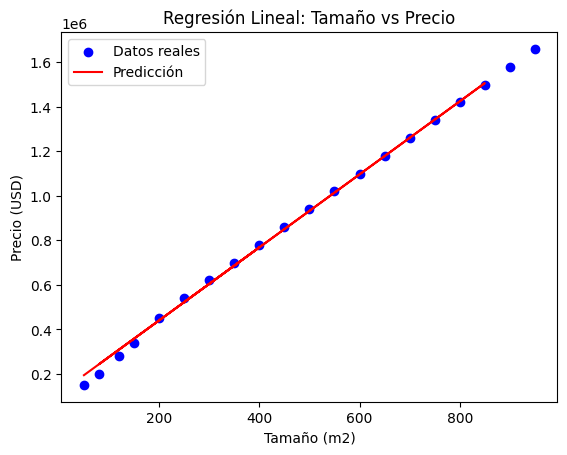
plt.title('Regresión Lineal: Tamaño vs Precio')
plt.show()
Error cuadrático medio (MSE): 714590725.8447672
###Explicación del código:
Generación de datos simulados: Creamos un conjunto de datos con dos columnas, Tamaño (m2) y Precio (USD), que representan el tamaño de la vivienda y su precio en dólares, respectivamente.
Variables de entrada y salida: Definimos X (variable independiente) como el tamaño y y (variable dependiente) como el precio.
División de datos: Dividimos los datos en un conjunto de entrenamiento (70%) y uno de prueba (30%) para evaluar el modelo.
Creación y entrenamiento del modelo: Usamos LinearRegression de sklearn para crear y entrenar el modelo con los datos de entrenamiento.
Predicción y evaluación: Utilizamos el modelo entrenado para predecir los precios del conjunto de prueba y calculamos el error cuadrático medio (MSE) para medir la precisión.
Visualización: Graficamos los datos reales y la línea de regresión para observar la relación entre el tamaño y el precio de las viviendas.
##Ejemplo 2: Clasificación de clientes en tienda (Clasificación Binaria)
Contexto: Este ejemplo utiliza la clasificación binaria para predecir si un cliente comprará o no en una tienda en función del tiempo que pasa en la tienda y la cantidad de productos que revisa. Esta es una típica aplicación de clasificación en el comercio, donde intentamos entender el comportamiento de los clientes.
# Importamos las bibliotecas necesarias
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
# Generamos un conjunto de datos ampliado
data = {
'Edad': [20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58,
21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59],
'Tiempo en tienda (min)': [5, 10, 15, 20, 25, 30, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70,
10, 15, 20, 25, 30, 35, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75],
'Compra': [0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
}
# Convertimos los datos a un DataFrame
df = pd.DataFrame(data)
# Definimos las variables de entrada (X) y de salida (y)
X = df[['Edad', 'Tiempo en tienda (min)']]
y = df['Compra']
# Dividimos los datos en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Creamos y entrenamos el modelo de regresión logística
modelo = LogisticRegression()
modelo.fit(X_train, y_train)
# Hacemos predicciones en el conjunto de prueba
y_pred = modelo.predict(X_test)
# Evaluamos el modelo
precision = accuracy_score(y_test, y_pred)
matriz_confusion = confusion_matrix(y_test, y_pred)
print("Precisión del modelo:", precision)
print("Matriz de confusión:")
print(matriz_confusion)
# Visualización de las predicciones
plt.figure(figsize=(8, 6))
sns.scatterplot(data=df, x='Edad', y='Tiempo en tienda (min)', hue='Compra', palette='coolwarm', edgecolor='k', s=100)
plt.title('Clasificación de clientes: 0 = Compra Baja, 1 = Compra Alta')
plt.xlabel('Edad')
plt.ylabel('Tiempo en tienda (min)')
plt.legend(title='Clase')
plt.show()
Precisión del modelo: 1.0
Matriz de confusión:
[[ 2 0]
[ 0 10]]
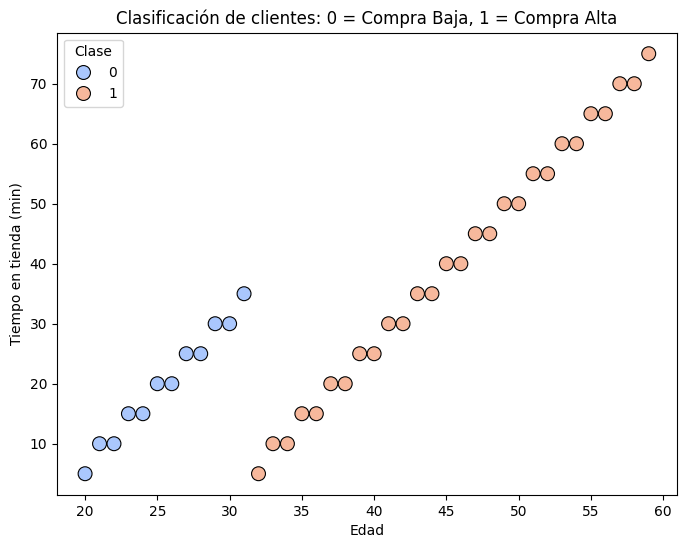
###Explicación del código:
Generación de datos simulados: Creamos datos que contienen el tiempo que los clientes pasan en la tienda, el número de productos que revisan, y si realizaron una compra (Compra = 1) o no (Compra = 0).
Definición de variables: X contiene las variables predictoras (Tiempo en tienda y Productos revisados), y y la variable objetivo (Compra).
División de datos: Dividimos los datos en conjuntos de entrenamiento y prueba.
Entrenamiento del modelo: Entrenamos un modelo de clasificación binaria con LogisticRegression.
Evaluación: Utilizamos el modelo para hacer predicciones y calculamos la precisión y la matriz de confusión para evaluar su desempeño.
##Ejemplo 3: Clasificación de correos electrónicos (Clasificación Binaria) Contexto: Este ejemplo aborda la clasificación binaria para predecir si un correo es «Spam» o «No Spam» en función de ciertas características textuales. Esta técnica se usa ampliamente en la clasificación de correos electrónicos y mensajes de texto.
# Importamos las bibliotecas necesarias
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
# Generamos un conjunto de datos ampliado
data = {
'Palabras en el correo': np.random.randint(50, 1000, 200),
'Frecuencia palabras de spam': np.random.uniform(0, 1, 200),
'Longitud del título': np.random.randint(5, 50, 200),
'Spam': np.random.choice([0, 1], 200, p=[0.7, 0.3])
}
# Convertimos los datos a un DataFrame
df = pd.DataFrame(data)
# Definimos las variables de entrada (X) y de salida (y)
X = df[['Palabras en el correo', 'Frecuencia palabras de spam', 'Longitud del título']]
y = df['Spam']
# Dividimos los datos en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Creamos y entrenamos el modelo de regresión logística
modelo = LogisticRegression()
modelo.fit(X_train, y_train)
# Hacemos predicciones en el conjunto de prueba
y_pred = modelo.predict(X_test)
# Evaluamos el modelo
precision = accuracy_score(y_test, y_pred)
matriz_confusion = confusion_matrix(y_test, y_pred)
print("Precisión del modelo:", precision)
print("Matriz de confusión:")
print(matriz_confusion)
# Visualización de las predicciones
plt.figure(figsize=(10, 6))
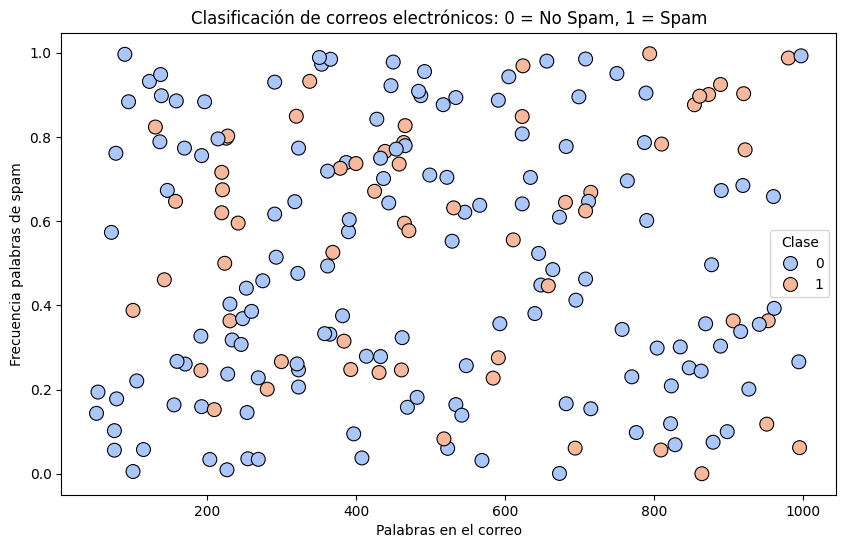
sns.scatterplot(data=df, x='Palabras en el correo', y='Frecuencia palabras de spam', hue='Spam', palette='coolwarm', edgecolor='k', s=100)
plt.title('Clasificación de correos electrónicos: 0 = No Spam, 1 = Spam')
plt.xlabel('Palabras en el correo')
plt.ylabel('Frecuencia palabras de spam')
plt.legend(title='Clase')
plt.show()
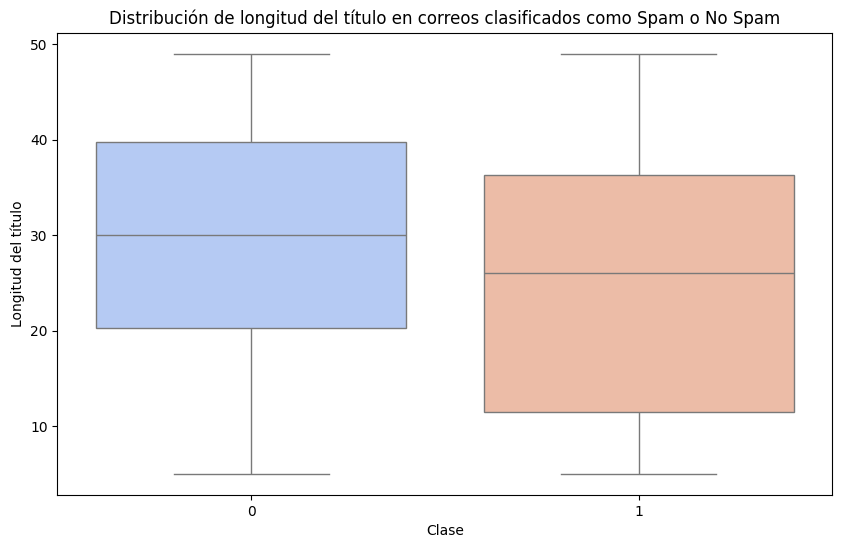
# Visualización adicional: Relación entre Longitud del título y Spam
plt.figure(figsize=(10, 6))
sns.boxplot(x='Spam', y='Longitud del título', data=df, hue='Spam', palette='coolwarm', dodge=False, legend=False)
plt.title('Distribución de longitud del título en correos clasificados como Spam o No Spam')
plt.xlabel('Clase')
plt.ylabel('Longitud del título')
plt.show()
Precisión del modelo: 0.6833333333333333
Matriz de confusión:
[[41 0]
[19 0]]
#Sección 4: Ejercicios de práctica ##1: Clasificación de frutas (Clasificación Binaria) Clasificar si una fruta es una manzana o una naranja utilizando características simples como el peso y el diámetro.
###Características:
peso en gramos
diámetro en centímetros
Objetivo: Entrenar un modelo de clasificación binaria para predecir si una fruta es una manzana (1) o una naranja (0) en función de sus características.
###Pseudocódigo:
Definir el conjunto de datos: Crear una lista de datos con el peso y diámetro de varias frutas, etiquetadas como manzana (1) o naranja (0).
Dividir el conjunto de datos en características (X) y etiquetas (y).
Separar el conjunto de datos en datos de entrenamiento y prueba.
Crear el modelo de regresión logística o un clasificador binario.
Entrenar el modelo con los datos de entrenamiento.
Evaluar el modelo utilizando los datos de prueba y calcular la precisión.
Visualizar los resultados con una gráfica de dispersión para observar la separación entre manzanas y naranjas en función del peso y diámetro.
##2: Clasificación de transacciones bancarias (Clasificación Binaria) Clasificar si una transacción bancaria es «fraudulenta» o «legítima» utilizando características como el monto y la frecuencia de la transacción.
###Características:
Monto de la transacción en dólares
Frecuencia de transacciones (número de transacciones en la última semana)
Objetivo: Entrenar un modelo de clasificación binaria para predecir si una transacción es fraudulenta (1) o legítima (0) en función de las características.
###Pseudocódigo:
Definir el conjunto de datos: Crear un conjunto de datos simulados de transacciones con las características de monto y frecuencia.
Dividir el conjunto de datos en características (X) y etiquetas (y).
Separar el conjunto de datos en entrenamiento y prueba.
Crear el modelo de regresión logística o un clasificador binario.
Entrenar el modelo con los datos de entrenamiento.
Evaluar el modelo utilizando el conjunto de prueba y calcular la precisión.
Visualizar los resultados en una gráfica de dispersión que muestre la clasificación entre transacciones fraudulentas y legítimas.
#Conclusión Este notebook te ha guiado a través de conceptos fundamentales del aprendizaje supervisado, aplicando técnicas como la regresión lineal y la clasificación binaria en ejemplos prácticos. A lo largo de estos ejercicios, has aprendido cómo implementar y aplicar modelos de Machine Learning para resolver problemas cotidianos, como la predicción de lluvia o la clasificación de transacciones. Estas técnicas te brindan una base sólida para abordar problemas más complejos en análisis de datos e inteligencia artificial, permitiéndote tomar decisiones informadas y respaldadas por datos en diversas áreas.

