Probabilidad

¡Bienvenidos al quinto notebook del curso de Computación Científica! En esta sesión, comenzaremos a explorar el mundo de la probabilidad y estadística computacional, abordando distribuciones de probabilidad fundamentales y sus aplicaciones en diversos campos. A través de ejemplos prácticos y gráficos ilustrativos, aprenderemos cómo modelar fenómenos reales utilizando herramientas computacionales. Con este notebook se busca ofrecer una comprensión tanto de los conceptos teóricos como de las implementaciones prácticas en Python, con aplicaciones que van desde la biología y medicina hasta las neurociencias y la actuaría.

2. Introducción a las distribuciones de probabilidad

Una distribución de probabilidad describe cómo se comportan las posibles salidas de una variable aleatoria. Puede ser discreta (como en el caso de la distribución binomial) o continua (como en el caso de la distribución normal). A lo largo de este notebook, estudiaremos algunas de las distribuciones más comunes y útiles en la estadística computacional, veremos su interpretación, su fórmula matemática y cómo aplicarlas a problemas reales.

Empecemos por algunas distribuciones discretas.

#3. Distribuciones discretas ##3.1 Distribución Bernoulli

La distribución Bernoulli describe un experimento que solo tiene dos resultados posibles: éxito (1) o fracaso (0). Un ejemplo clásico sería el lanzamiento de una moneda, donde 1 representa «cara» y 0 representa «cruz». La probabilidad de éxito se denota por ( p ), y la de fracaso por ( 1 - p ).

\[ P(X=1) = p \quad y \quad P(X=0) = 1-p \]

Ejemplo:

Podemos usar una distribución Bernoulli para modelar si un paciente responde o no a un tratamiento (éxito o fracaso).

import numpy as np
import matplotlib.pyplot as plt

# Simulamos 1000 resultados de una variable aleatoria Bernoulli con p=0.4
# La distribución Bernoulli genera resultados binarios (0 o 1) basados en una probabilidad p.
# np.random.binomial(n, p, size) genera resultados de una distribución binomial.
# Si ponemos n=1, tenemos una distribución Bernoulli (caso especial de la binomial).
# p=0.4 significa que la probabilidad de éxito (1) es 40%, y la probabilidad de fracaso (0) es 60%.
n = 1000  # Número de simulaciones (1000 experimentos)
p = 0.4   # Probabilidad de éxito en cada experimento
bernoulli = np.random.binomial(1, p, n)  # Genera 1000 resultados de Bernoulli con p=0.4

# Graficamos los resultados
# plt.hist() crea un histograma. Representamos cuántas veces obtenemos 0 (fracaso) y cuántas veces obtenemos 1 (éxito).
# bins=2 especifica que el histograma tendrá 2 barras (una para cada posible resultado: 0 y 1).
# rwidth=0.8 ajusta el ancho de las barras para que no ocupen todo el espacio, dejándolas un poco separadas (mejora la visualización).
plt.hist(bernoulli, bins=2, color='skyblue', rwidth=0.8)  # Graficamos un histograma de los resultados de Bernoulli
plt.title('Distribución Bernoulli: p=0.4')  # Título de la gráfica
plt.show()  # Muestra la gráfica

##3.2 Distribución Binomial

La distribución binomial es una extensión de la Bernoulli, donde realizamos ( n ) ensayos independientes, cada uno con la misma probabilidad de éxito ( p ). Un ejemplo clásico es lanzar una moneda varias veces y contar cuántas veces sale cara.

\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k} \]

Ejemplo:

La distribución binomial es útil en actuaría para modelar eventos de éxito o fracaso, donde el éxito puede interpretarse como la ocurrencia de un siniestro o reclamo. Imagina que cada póliza de seguro tiene una probabilidad independiente p de que ocurra un siniestro durante el periodo cubierto. Si una compañía de seguros tiene n pólizas, la distribución binomial puede modelar el número de siniestros que ocurren, considerando que cada siniestro es independiente de los demás y que la probabilidad de que ocurra es la misma para todas las pólizas.

Por ejemplo:

Si una compañía de seguros tiene 10,000 pólizas de seguros de vida, y la probabilidad de que una póliza genere un reclamo es 0.01 (1%), la distribución binomial puede modelar cuántos reclamos habrá en total para esas 10,000 pólizas en un año. Aquí, el «éxito» sería que una póliza genere un reclamo, y el «fracaso» sería que no lo haga. Este tipo de análisis es fundamental para el cálculo de primas, reserva de siniestros y modelos de riesgos.

n_trials = 10  # Número de ensayos (cantidad de intentos en cada simulación)
p = 0.5        # Probabilidad de éxito en cada ensayo
n = 1000       # Número de simulaciones a realizar
binomial = np.random.binomial(n_trials, p, n)  # Genera n simulaciones de la distribución binomial

# Graficamos
plt.hist(binomial, bins=n_trials, color='orange', rwidth=0.8)  # Crea un histograma de los resultados
plt.title('Distribución Binomial con p=0.5 y n_trials=10')  # Añade el título a la gráfica
plt.show()  # Muestra la gráfica

#4. Distribuciones continuas ##4.1 Distribución Uniforme

La distribución uniforme describe una situación en la que todas las salidas posibles tienen la misma probabilidad de ocurrir. Un ejemplo clásico es un dado justo, donde cada cara tiene la misma probabilidad de salir.

\[ f(x) = \frac{1}{b-a} \quad \text{para} \quad a \leq x \leq b \]

Ejemplo:

En el ámbito de ciencias de la tierra, la distribución uniforme se puede usar para simular posiciones aleatorias de puntos en un terreno. Por ejemplo, si quisiéramos representar la ubicación de puntos de muestreo en una zona específica de terreno, podríamos asumir que la probabilidad de que un punto esté en cualquier lugar dentro de ese rango es igual.

# Definimos el límite inferior y superior de la distribución uniforme
a, b = 0, 10  # Limite inferior y superior

# Generamos 1000 valores aleatorios siguiendo una distribución uniforme entre a y b
uniforme = np.random.uniform(a, b, 1000)

# Graficamos la distribución generada
# 'bins=30' define la cantidad de barras que tendrá el histograma
# 'color="orange"' asigna el color de las barras
# 'rwidth=0.8' define el ancho relativo de las barras, aquí es 80% del espacio disponible
plt.hist(uniforme, bins=30, color='orange', rwidth=0.8)
plt.title('Distribución Uniforme entre 0 y 10')
plt.show()

##4.2. Distribución Normal

La distribución normal es la distribución continua más común. Su forma característica es la «campana de Gauss». Está completamente definida por su media ( \mu ) y su desviación estándar ( \sigma ).

\[ f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

Ejemplo:

En neurociencias, la distribución normal se utiliza para modelar el comportamiento de la actividad neuronal, ya que muchas variables biológicas tienden a seguir un patrón normal o «campana». Por ejemplo, se puede modelar la variabilidad de las sinapsis neuronales (los puntos de conexión entre las neuronas) en ciertas regiones del cerebro. La sinapsis es esencial para la transmisión de señales eléctricas entre las neuronas, y su actividad puede fluctuar debido a factores fisiológicos. Cuando se estudian los tiempos entre disparos neuronales o la intensidad de esos disparos en determinadas áreas, muchas veces estos datos siguen una distribución normal.

En este ejemplo, la distribución de los disparos neuronales (activaciones sinápticas) de una región cerebral específica se puede aproximar a una distribución normal estándar. El eje horizontal representará las desviaciones estándar de la actividad (de -3 a 3), mientras que el eje vertical representará la frecuencia de observación de cada valor de actividad.

import numpy as np
import matplotlib.pyplot as plt

# Definimos la media (mu) y la desviación estándar (sigma) de la distribución normal
mu, sigma = 0, 1  # Esto significa que es una distribución normal estándar

# Simulamos 1000 puntos que siguen esta distribución normal
normal = np.random.normal(mu, sigma, 1000)

# Graficamos la distribución de los puntos simulados
plt.hist(normal, bins=30, color='green', rwidth=0.8)

# Añadimos títulos y etiquetas para que la gráfica sea más clara
plt.title('Distribución Normal Estándar: Actividad Neuronal')
plt.xlabel('Intensidad de Actividad (en desviaciones estándar)')
plt.ylabel('Frecuencia')

# Mostramos la gráfica
plt.show()

##4.3 Distribución Exponencial

La distribución exponencial modela el tiempo que transcurre entre eventos que ocurren a una tasa constante.

\[ f(x) = \lambda e^{-\lambda x} \quad \text{para} \quad x \geq 0 \]

Ejemplo:

La distribución exponencial es útil en biología para modelar el tiempo de vida de organismos bajo condiciones controladas, donde el riesgo de muerte es constante. Esto significa que, sin importar cuánto tiempo haya vivido un organismo, su probabilidad de morir en un pequeño intervalo de tiempo sigue siendo la misma. Un ejemplo típico sería modelar el tiempo de vida de bacterias bajo un ambiente controlado donde la tasa de mortalidad es constante.

import numpy as np
import matplotlib.pyplot as plt

# Definimos el parámetro lambda que controla la tasa a la cual ocurren los eventos
# Aquí, lambda_param representa la tasa de mortalidad, por lo que 1/lambda_param es el tiempo medio de vida
lambda_param = 1.0

# Simulamos 1000 tiempos de vida de organismos utilizando la distribución exponencial
exponencial = np.random.exponential(1/lambda_param, 1000)

# Graficamos los resultados
plt.hist(exponencial, bins=30, color='purple', rwidth=0.8)
plt.title('Distribución Exponencial: Modelando el Tiempo de Vida de Organismos')
plt.xlabel('Tiempo de vida (días)')
plt.ylabel('Frecuencia de organismos')
plt.show()

#5. Distribuciones avanzadas ##5.1 Distribución Gamma

La distribución Gamma generaliza la exponencial y se utiliza para modelar el tiempo hasta que ocurren varios eventos independientes.

\[ f(x) = \frac{x^{k-1} e^{-x/\theta}}{\theta^k \Gamma(k)} \]

###Ejemplo: En el campo de la medicina, la distribución Gamma se utiliza para modelar eventos que tienen una tasa variable de ocurrencia, como el tiempo de supervivencia de pacientes después de someterse a ciertos tratamientos. Esta distribución puede ayudar a predecir cuánto tiempo podrían sobrevivir los pacientes bajo condiciones específicas, como en ensayos clínicos.

###¿Cómo funciona? La distribución Gamma se caracteriza por dos parámetros:

Shape (Forma): Controla cuántos subeventos ocurren antes de que el evento principal (por ejemplo, la muerte o el alta del paciente) se complete.

Scale (Escala): Relaciona la duración media de cada uno de estos subeventos. En este contexto, la distribución Gamma nos permite observar cómo varía el tiempo de supervivencia. Supongamos que estamos midiendo la respuesta de los pacientes a un tratamiento específico. Con los datos obtenidos, podemos ajustar un modelo de distribución Gamma para predecir cómo se comportará la supervivencia del paciente.

Gráfica de la Distribución Gamma

El siguiente gráfico muestra cómo se distribuye el tiempo de supervivencia de los pacientes sometidos a este tratamiento en particular.

# Definimos los parámetros de la distribución Gamma
shape_param = 2  # Parámetro de forma
scale_param = 2  # Parámetro de escala

# Simulamos 1000 tiempos de supervivencia de pacientes según esta distribución
gamma = np.random.gamma(shape_param, scale_param, 1000)

# Graficamos los resultados
plt.hist(gamma, bins=30, color='gold', rwidth=0.8)
plt.title('Distribución Gamma (shape=2, scale=2)')
plt.xlabel('Tiempo de supervivencia (meses)')
plt.ylabel('Número de pacientes')
plt.show()

###5.2 La distribución Poisson Modela la probabilidad de que ocurra un número determinado de eventos en un intervalo de tiempo fijo o en un área dada, cuando los eventos ocurren de manera independiente. Es especialmente útil cuando los eventos son raros, como la ocurrencia de terremotos o llamadas a un centro de atención telefónica.

Ejemplo:

En neurociencia, la distribución Poisson puede usarse para modelar la tasa de disparos de una neurona en una red neuronal.

Fórmula:

\[ P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} \]

Donde:

λ es la tasa promedio de eventos en un intervalo fijo de tiempo o espacio.

𝑘 es el número de eventos.

from scipy.stats import poisson

# Definimos la tasa de ocurrencia (lambda)
lambda_param = 5

# Creamos los valores de k
x = np.arange(0, 20)

# Obtenemos la distribución Poisson
poisson_dist = poisson.pmf(x, lambda_param)

# Graficamos
plt.bar(x, poisson_dist, color='purple')
plt.title(f'Distribución Poisson (lambda={lambda_param})')
plt.xlabel('Número de eventos (k)')
plt.ylabel('Probabilidad')
plt.show()

#5.3 Distribución Log-Normal La distribución Log-Normal es utilizada cuando los datos no siguen una distribución normal, pero la transformación logarítmica de los mismos sí lo hace. Es útil en finanzas y biología, donde a menudo modela el crecimiento de poblaciones o precios de activos.

Ejemplo:

En economía, la distribución Log-Normal puede modelar la distribución de los ingresos en una población, ya que las variaciones en ingresos suelen ser multiplicativas.

Fórmula:

\[f(x|\mu,\sigma) = \frac{1}{x\sigma \sqrt{2\pi}} e^{-\frac{(\ln x - \mu)^2}{2\sigma^2}}\]

from scipy.stats import lognorm

# Definimos los parámetros de la distribución Log-Normal
mu, sigma = 0, 0.1

# Creamos los valores de x
x = np.linspace(0, 5, 1000)

# Obtenemos la función de densidad de probabilidad
lognormal_dist = lognorm.pdf(x, sigma, scale=np.exp(mu))

# Graficamos
plt.plot(x, lognormal_dist, label='Distribución Log-Normal', color='orange')
plt.title('Distribución Log-Normal')
plt.xlabel('x')
plt.ylabel('Densidad de probabilidad')
plt.legend()
plt.show()

##5.4 Distribución t de Student La distribución t de Student es útil cuando estamos trabajando con muestras pequeñas y no conocemos la varianza poblacional. Se usa principalmente en pruebas de hipótesis, como el t-test, donde comparamos si dos grupos tienen medias diferentes. Es fundamental en estadística inferencial y tiene una mayor dispersión que la normal, especialmente con pocos grados de libertad.

Ejemplo:

En el contexto de investigación médica, podríamos utilizar la t de Student para analizar si un nuevo fármaco reduce más la presión arterial que un placebo, tomando en cuenta una muestra pequeña de pacientes.

Fórmula:

\[ f(t, \nu) = \frac{\Gamma \left( \frac{\nu + 1}{2} \right)}{\sqrt{\nu \pi} \Gamma \left( \frac{\nu}{2} \right)} \left( 1 + \frac{t^2}{\nu} \right)^{-\frac{\nu + 1}{2}} \]

Donde:

• \(\nu\) es el número de grados de libertad.

from scipy.stats import t
import matplotlib.pyplot as plt
import numpy as np

# Definimos los grados de libertad
df = 10  # Grados de libertad

# Creamos los valores de t
x = np.linspace(-5, 5, 1000)

# Obtenemos la función de densidad de probabilidad
t_dist = t.pdf(x, df)

# Graficamos
plt.plot(x, t_dist, label=f't-student (df={df})', color='blue')
plt.title('Distribución t de Student')
plt.xlabel('t')
plt.ylabel('Densidad de probabilidad')
plt.legend()
plt.show()

from scipy.stats import f

# Definimos los grados de libertad del numerador y denominador
dfn, dfd = 5, 10

# Creamos los valores de F
x = np.linspace(0, 5, 1000)

# Obtenemos la función de densidad de probabilidad
f_dist = f.pdf(x, dfn, dfd)

# Graficamos
plt.plot(x, f_dist, label=f'F (dfn={dfn}, dfd={dfd})', color='green')
plt.title('Distribución F')
plt.xlabel('F')
plt.ylabel('Densidad de probabilidad')
plt.legend()
plt.show()

##5.5 Distribución F La distribución F es utilizada principalmente en pruebas de hipótesis como el ANOVA para comparar varianzas entre múltiples grupos. Esta distribución es asimétrica y depende de dos parámetros: los grados de libertad del numerador y del denominador.

Ejemplo:

En estudios de biología y agricultura, se puede usar la distribución F para comparar la efectividad de distintos fertilizantes sobre el crecimiento de las plantas.

Fórmula:

\[f(x; d_1, d_2) = \frac{\left( \frac{d_1}{d_2} \right)^{d_1/2} x^{(d_1/2) - 1}}{\left( 1 + \frac{d_1}{d_2}x \right)^{(d_1 + d_2)/2} B\left( \frac{d_1}{2}, \frac{d_2}{2} \right)}\]

Donde: \(d_1\) y \(d_2\) son los grados de libertad del numerador y denominador, respectivamente.

#Ejercicios de Práctica ##Ejercicio 1: Distribución Binomial En el área de enfermería, una parte fundamental del trabajo clínico es la observación y el registro de los efectos secundarios tras la administración de vacunas y medicamentos. En los ensayos clínicos de vacunas, como las que se desarrollaron para COVID-19, los efectos secundarios leves son monitoreados de cerca para garantizar la seguridad y eficacia de las vacunas antes de que se distribuyan a la población general.

En este ejercicio, vamos a utilizar la distribución binomial para modelar la cantidad de pacientes que presentan efectos secundarios leves tras recibir una vacuna experimental contra COVID-19. Este tipo de modelado es útil para prever la cantidad de pacientes que pueden necesitar cuidados de seguimiento tras la administración de la vacuna, lo que a su vez ayuda a planificar los recursos necesarios en un centro de salud.

Situación: En un ensayo clínico, se vacuna a 1000 personas y sabemos que la probabilidad de que un paciente experimente efectos secundarios leves es del 30%.

Utiliza una distribución binomial para modelar cuántos pacientes presentarán efectos secundarios, y grafica los resultados para observar la distribución.

Tarea:

Simula la cantidad de pacientes que podrían tener efectos secundarios en un ensayo clínico utilizando la distribución binomial.

Grafica los resultados para visualizar cuántos pacientes presentan efectos secundarios.

Asegúrate de que la gráfica sea clara y describa adecuadamente los datos para poder presentar los resultados de manera entendible para el equipo de salud.

import numpy as np
import matplotlib.pyplot as plt

# Parámetros del experimento
n_pacientes = 1000  # Número de personas en el ensayo clínico
p_efectos_secundarios = 0.3  # Probabilidad de que un paciente tenga efectos secundarios

# Simulamos el número de personas con efectos secundarios usando la distribución binomial
efectos_secundarios = np.random.binomial(n_pacientes, p_efectos_secundarios, 1000)

# Graficamos los resultados
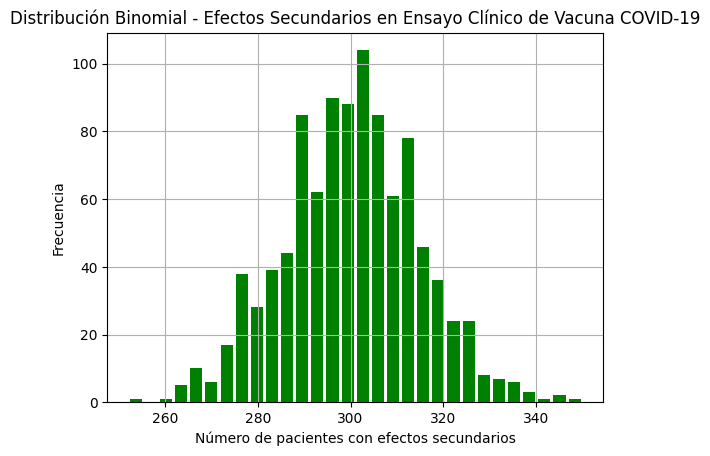
plt.hist(efectos_secundarios, bins=30, color='green', rwidth=0.8)
plt.title('Distribución Binomial - Efectos Secundarios en Ensayo Clínico de Vacuna COVID-19')
plt.xlabel('Número de pacientes con efectos secundarios')
plt.ylabel('Frecuencia')
plt.grid(True)
plt.show()

import numpy as np
import matplotlib.pyplot as plt

# Parámetros del problema
n_pacientes = ____  # Número de pacientes vacunados
prob_efectos_secundarios = ___  # Probabilidad de efectos secundarios graves

# Simulación de la distribución binomial para el número de pacientes con efectos secundarios graves
pacientes_con_efectos = np.random.binomial(n_pacientes, prob_efectos_secundarios, size=_____)

# Gráfico de la distribución
plt.hist(pacientes_con_efectos, bins=30, color='#006400', rwidth=0.85)
plt.title('Simulación de Efectos Secundarios Graves por la Vacuna contra COVID-19\nDistribución del Número de Pacientes con Efectos Secundarios en _____ Ensayos')
plt.xlabel('Número de Pacientes con Efectos Secundarios Graves')
plt.ylabel('Número de Simulaciones con esa Cantidad de Pacientes')
plt.grid(axis='y', alpha=0.75)

plt.show()

##Ejercicio 2: Distribución Normal Contexto: Estás trabajando en un laboratorio donde se mide la radiación emitida por una fuente de partículas durante 24 horas. Se sabe que los datos de radiación tienden a seguir una distribución normal con una media de 50 unidades de radiación y una desviación estándar de 5 unidades. Quieres simular los datos para entender mejor el comportamiento de la fuente y detectar anomalías.

Instrucciones:

Simula 1000 mediciones de la radiación usando una distribución normal con los parámetros dados (media de 50 y desviación estándar de 5).

Grafica un histograma de las mediciones y verifica si los datos simulan correctamente lo esperado.

Comenta si algún valor fuera de lo común podría interpretarse como una posible anomalía.

Indicaciones:

Media = 50

Desviación estándar = 5

import numpy as np
import matplotlib.______ as plt

# Parámetros de la distribución
mu = __  # Media de la radiación
sigma = _  # Desviación estándar de la radiación
n_mediciones = ___  # Número de mediciones

# Simulamos las mediciones de radiación
radiacion = np.random.______(mu, sigma, n_mediciones)

# Graficamos el histograma de las mediciones
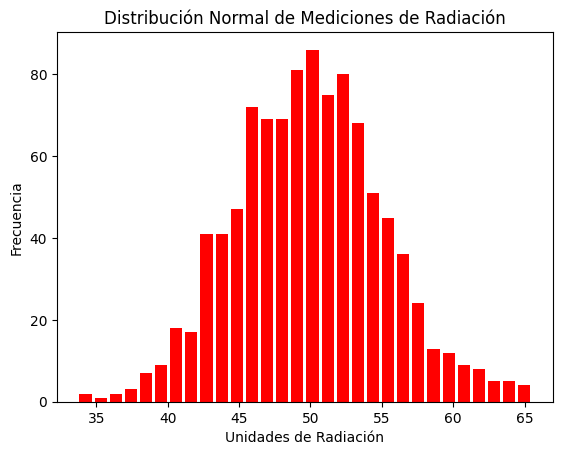
plt.____(radiacion, bins=30, color='red', rwidth=0.8)
plt.title('Distribución Normal de Mediciones de Radiación')
plt.xlabel('Unidades de Radiación')
plt.ylabel('Frecuencia')
plt.show()

##Ejercicio 3: Distribución Gamma (Avanzado) Contexto: En un hospital, se está investigando la duración de supervivencia de pacientes sometidos a un nuevo tratamiento experimental contra el cáncer. Se ha determinado que la duración del tratamiento sigue una distribución gamma con los parámetros de forma (𝑘) y escala (𝜃). Quieres modelar cuánto tiempo puede sobrevivir un paciente promedio bajo este tratamiento.

Instrucciones:

1. Simula el tiempo de supervivencia de 500 pacientes usando una distribución gamma con 𝑘=2 y 𝜃=1.5.

2. Grafica los resultados e interpreta el tiempo promedio de supervivencia.

3. ¿Qué implicaciones tiene esto para la planificación de tratamientos a largo plazo?

Indicaciones:

Parámetro de forma 𝑘=2

Parámetro de escala 𝜃=1.5

import _____ as np
import matplotlib.pyplot as plt

# Parámetros de la distribución Gamma
shape_param = _ # Parámetro de forma (k)
scale_param = ___  # Parámetro de escala (θ)
n_pacientes = ___  # Número de pacientes

# Simulamos el tiempo de supervivencia de los pacientes
supervivencia = np.random.gamma(shape_param, scale_param, n_pacientes)

# Graficamos el histograma de los resultados
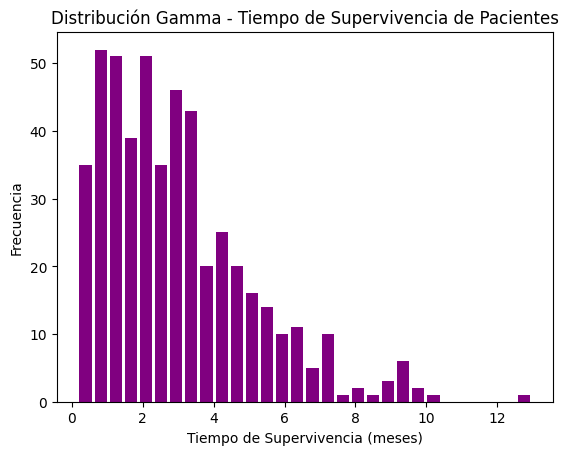
plt.hist(supervivencia, bins=__, color='purple', rwidth=0.8)
plt.title('Distribución Gamma - Tiempo de Supervivencia de Pacientes')
plt.xlabel('Tiempo de Supervivencia (meses)')
plt.ylabel('Frecuencia')
plt.show()

# Calculamos el tiempo promedio de supervivencia
tiempo_promedio = np.mean(supervivencia)
print(f'Tiempo promedio de supervivencia: {tiempo_promedio:.2f} meses')

Tiempo promedio de supervivencia: 2.96 meses

##Ejercicio 4: Distribución t de Student (avanzado) Contexto: Estás investigando el rendimiento de dos algoritmos de machine learning para detectar fallas en una red de telecomunicaciones. Después de varias pruebas, tienes dos muestras de tiempos de ejecución en milisegundos y quieres comparar si hay una diferencia significativa entre ellas. Para esto, usarás la distribución t de Student para realizar una prueba de hipótesis sobre la diferencia entre las medias de los tiempos.

\ Instrucciones:

Simula dos conjuntos de datos de tiempos de ejecución (n = 50 para cada algoritmo) usando una distribución normal.

Media del algoritmo 1 = 100 ms, Desviación estándar = 10 ms.

Media del algoritmo 2 = 102 ms, Desviación estándar = 12 ms.

Realiza una prueba t para determinar si hay una diferencia significativa entre los tiempos de los dos algoritmos.

Interpreta los resultados de la prueba t y comenta si esta empresa de telecomunicaciones debería cambiar de algoritmo.

\ Indicaciones:

Usa una prueba t para dos muestras independientes.

import numpy as __
from scipy import stats
import matplotlib.pyplot as ___

# Parámetros de las distribuciones normales para cada algoritmo
mu_algoritmo_1 = ___  # Media del tiempo de ejecución del algoritmo 1
sigma_algoritmo_1 = __  # Desviación estándar del algoritmo 1
mu_algoritmo_2 = ___  # Media del tiempo de ejecución del algoritmo 2
sigma_algoritmo_2 = __  # Desviación estándar del algoritmo 2
n = __  # Número de ejecuciones simuladas para cada algoritmo

# Simulamos los tiempos de ejecución para ambos algoritmos
tiempos_algoritmo_1 = np.______.normal(mu_algoritmo_1, sigma_algoritmo_1, n)
tiempos_algoritmo_2 = __.random.______(mu_algoritmo_2, sigma_algoritmo_2, n)

# Realizamos una prueba t de Student para dos muestras independientes
t_stat, p_value = stats.ttest_ind(tiempos_algoritmo_1, tiempos_algoritmo_2)

# Mostramos los resultados de la prueba t
print(f'Estadístico t: {t_stat:.2f}')
print(f'Valor p: {p_value:.4f}')

# Interpretamos el resultado
if p_value < 0.05:
    print("Existe una diferencia significativa entre los tiempos de los algoritmos.")
else:
    _____("No existe una diferencia significativa entre los tiempos de los algoritmos.")

# Graficamos los tiempos de ambos algoritmos
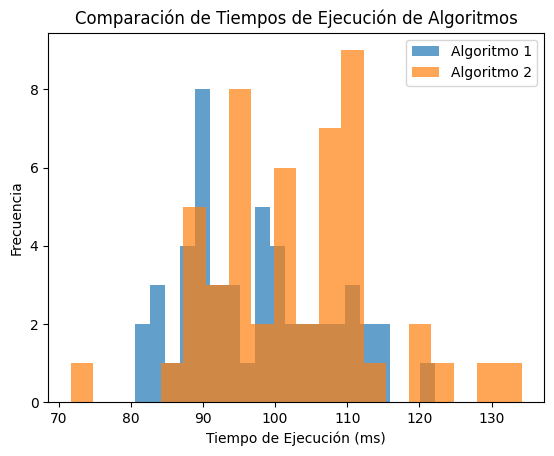
plt.hist(tiempos_algoritmo_1, bins=20, alpha=0.7, label='Algoritmo 1')
plt.hist(tiempos_algoritmo_2, bins=20, alpha=0.7, label='Algoritmo 2')
plt.title('Comparación de Tiempos de Ejecución de Algoritmos')
plt.xlabel('Tiempo de Ejecución (ms)')
plt.ylabel('Frecuencia')
plt.legend()
plt.show()

Estadístico t: -2.41
Valor p: 0.0178
Existe una diferencia significativa entre los tiempos de los algoritmos.

#7. Conclusión En este notebook, hemos cubierto una amplia gama de distribuciones de probabilidad y hemos simulado aplicaciones a problemas en campos tan diversos como la biología, la medicina, las neurociencias y la actuaría. A lo largo de este recorrido, hemos trabajado con distribuciones continuas y discretas, y hemos implementado simulaciones para obtener una comprensión más clara de las herramientas estadísticas. Recuerda que estos conceptos son esenciales en la toma de decisiones informadas y en la interpretación correcta de datos en el ámbito profesional.