Estadística descriptiva

Introducción

En este notebook vamos a profundizar en las herramientas y conceptos clave de la estadística descriptiva, que nos permiten resumir y entender los datos de manera efectiva. La estadística descriptiva no solo se limita a las medidas de tendencia central (media, mediana y moda) que ya hemos visto, sino que incluye medidas de dispersión, de forma, y otras formas de caracterizar un conjunto de datos. Estas herramientas son fundamentales en diversas áreas, desde la medicina hasta la biología, pasando por ciencias de la computación y actuaría. Vamos a explorar estas herramientas, acompañadas de ejemplos claros y aplicables.

##Contenido:

1. Medidas de Dispersión:

• Rango

• Varianza

• Desviación estándar

• Coeficiente de variación

• Percentiles y cuartiles

2. Medidas de Forma:

• Asimetría

• Curtosis

3. Representación gráfica:

• Boxplots (gráficos de cajas y bigotes)

• Histogramas (ya visto en notebooks anteriores)

• Diagramas de dispersión

#1. Medidas de dispersión Las medidas de dispersión nos indican cómo están distribuidos los datos alrededor de la media o de otros puntos de referencia.

##Rango El rango es simplemente la diferencia entre el valor más grande y el más pequeño de un conjunto de datos. Es útil cuando queremos tener una idea rápida de la amplitud de los datos, aunque puede ser muy sensible a los valores atípicos.

###Ejemplo: El rango de las edades de los pacientes en una unidad de cuidados intensivos puede darnos una idea general del perfil de edad. Si el paciente más joven tiene 25 años y el más viejo 75, el rango sería de 50 años. Esto puede ayudar a gestionar mejor los recursos médicos.

# Ejemplo en enfermería: Rango de edades de pacientes
edades = [25, 35, 45, 55, 65, 75]
rango = max(edades) - min(edades)
print(f"El rango de edades de los pacientes es: {rango} años")

##Varianza y desviación estándar La varianza mide cómo se distribuyen los datos alrededor de la media. Es la media de las diferencias al cuadrado entre los valores y la media.

La desviación estándar es simplemente la raíz cuadrada de la varianza y nos da una medida más interpretable, ya que está en las mismas unidades que los datos originales.

###Ejemplo: Supongamos que estamos midiendo el nivel de azúcar en sangre de un grupo de pacientes. La desviación estándar nos puede ayudar a entender qué tan dispersos están los niveles de azúcar alrededor de la media. Un valor alto indicaría que algunos pacientes tienen niveles muy por encima o por debajo del promedio.

# Ejemplo: Niveles de azúcar en sangre
import numpy as np

niveles_azucar = [85, 90, 95, 100, 110, 120, 130]
varianza = np.var(niveles_azucar)
desviacion_estandar = np.std(niveles_azucar)
print(f"Varianza: {varianza}, Desviación estándar: {desviacion_estandar}")

##Coeficiente de variación Es una medida de dispersión relativa que compara la desviación estándar con la media, expresado en porcentaje. Es útil cuando queremos comparar la variabilidad de dos o más grupos de datos con medias diferentes.

##Ejemplo: En estudios sobre la biodiversidad, el coeficiente de variación puede ser útil para comparar la variabilidad en el tamaño de diferentes especies de plantas, que podrían tener medias diferentes de altura.

# Ejemplo: Tamaño de plantas
altura_plantas = [15, 18, 22, 25, 27, 30]
media_altura = np.mean(altura_plantas)
cv = np.std(altura_plantas) / media_altura
print(f"Coeficiente de variación: {cv:.2f}")

##Percentiles y cuartiles Los percentiles dividen los datos en 100 partes iguales, mientras que los cuartiles los dividen en 4. El percentil 50 es equivalente a la mediana.

###Ejemplo: En un examen, si un estudiante está en el percentil 90, significa que el 90% de los estudiantes tienen una calificación igual o inferior a la suya. Esto es una medida de posición relativa útil en evaluaciones educativas.

# Ejemplo en matemáticas: Percentiles de calificaciones
calificaciones = [60, 70, 75, 80, 85, 90, 95]
percentil_90 = np.percentile(calificaciones, 90)
print(f"Percentil 90: {percentil_90}")

#2. Medidas de forma Además de las medidas de dispersión, podemos utilizar medidas de forma como la asimetría y la curtosis para entender mejor la distribución de los datos.

##Asimetría

La asimetría mide la simetría de la distribución de los datos. Una distribución simétrica tiene un valor de asimetría cercano a 0.

###Ejemplo: Si estamos midiendo las temperaturas diarias en una región y encontramos una asimetría positiva, esto podría significar que hay más días con temperaturas más frías y algunos días extremadamente calurosos.

import scipy.stats as stats  # Importamos la librería necesaria para calcular la asimetría

# Ejemplo: Temperaturas diarias
temperaturas = [20, 21, 22, 22, 23, 24, 25, 40]  # Día extremadamente caluroso al final
asimetria = stats.skew(temperaturas)
print(f"Asimetría: {asimetria:.2f}")

##Curtosis La curtosis mide si la distribución de los datos tiene colas más pesadas o ligeras en comparación con una distribución normal. Una curtosis positiva indica colas más pesadas.

###Ejemplo: Al analizar la duración de las hospitalizaciones, una curtosis positiva podría indicar que, aunque la mayoría de los pacientes tienen estancias cortas, algunos permanecen hospitalizados por periodos mucho más largos.

# Ejemplo: Duración de hospitalizaciones
hospitalizaciones = [3, 4, 5, 6, 7, 8, 9, 30]  # Pacientes con estancia prolongada
curtosis = stats.kurtosis(hospitalizaciones)
print(f"Curtosis: {curtosis:.2f}")

#3. Representación gráfica ##Boxplots Un boxplot es una excelente herramienta para visualizar la dispersión de los datos y detectar valores atípicos.

###Ejemplo: Los boxplots pueden ayudar a visualizar las respuestas neuronales a un estímulo en un experimento.

import matplotlib.pyplot as plt
# Ejemplo en neurociencias: Boxplot de respuestas neuronales
respuestas_neuronales = [10, 12, 14, 14, 15, 18, 19, 20, 22, 24, 100]  # Valor atípico en la respuesta
plt.boxplot(respuestas_neuronales)
plt.title("Boxplot de Respuestas Neuronales")
plt.show()

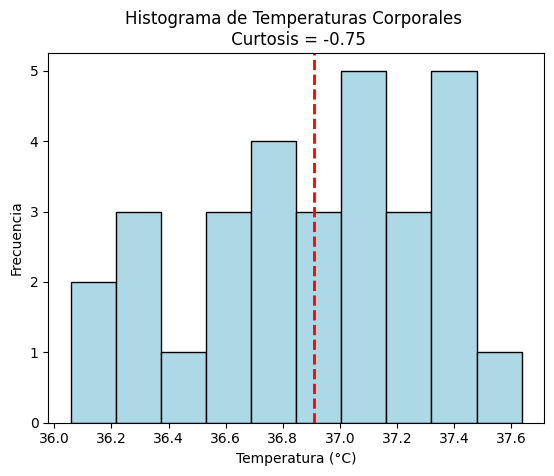
#4. Ejercicios ##Ejercicio 1: Curtosis En este ejercicio, vamos a analizar los datos de temperatura corporal de un grupo de pacientes de una unidad de cuidados intensivos. Supongamos que los datos de temperatura se registran varias veces al día. Queremos analizar la curtosis para identificar si las mediciones tienen una distribución más o menos plana o más o menos picuda en comparación con una distribución normal.

Los valores de curtosis nos indican cómo son las colas de la distribución en comparación con la distribución normal:

Curtosis positiva: la distribución tiene colas más pesadas (más valores extremos).

Curtosis negativa: la distribución tiene colas más ligeras.

Instrucciones:

1. Simula los datos de temperatura corporal para un grupo de 30 pacientes.

2. Calcula la curtosis de los datos.

3. Grafica un histograma de los datos de temperatura y añade una línea que marque la media.

import _ as _
import _ as _
from scipy.stats import ________

# Datos de temperatura corporal en pacientes (en °C)
temperaturas = np.random.normal(37, 0.5, 30)  # Temperaturas alrededor de 37°C

# Calculamos la curtosis
curtosis = kurtosis(_______)

# Graficamos
plt.hist(temperaturas, bins=10, color='lightblue', edgecolor='black')
plt.axvline(np.mean(temperaturas), color='red', linestyle='dashed', linewidth=2)
plt.title(f"Histograma de Temperaturas Corporales \n Curtosis = {curtosis:.2f}")
plt.xlabel("Temperatura (°C)")
plt.ylabel("Frecuencia")
plt.show()

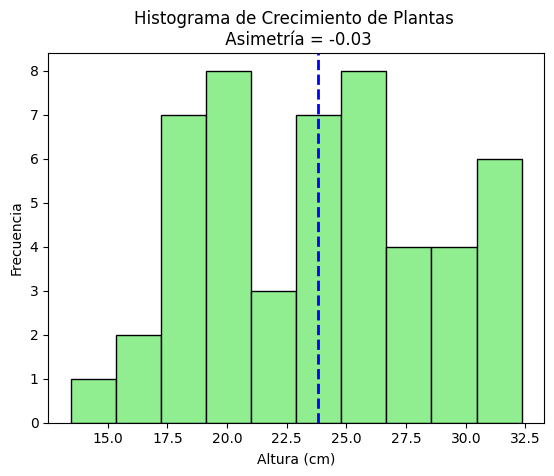
##Ejercicio 2: Asimetría - crecimiento de plantas En biología, a menudo se mide el crecimiento de plantas bajo diferentes condiciones. Supongamos que estás investigando el crecimiento de un grupo de plantas que se riegan con diferentes cantidades de agua. Los datos de crecimiento pueden mostrar asimetría dependiendo de las condiciones ambientales.

La asimetría mide si los datos están distribuidos simétricamente. Una asimetría positiva indica que la cola derecha es más larga, mientras que una negativa indica que la cola izquierda es más larga.

Instrucciones:

1. Simula datos de crecimiento en altura (en cm) para 50 plantas.

2. Calcula la asimetría de los datos.

3. Grafica un histograma y añade una línea de la media.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ____

# Datos simulados de crecimiento de plantas (en cm)
crecimiento = np.random.normal(25, 5, 50)  # Crecimiento promedio de 25 cm con desviación estándar de 5 cm

# Calculamos la asimetría
asimetria = skew(_______)

# Graficamos
plt.hist(crecimiento, bins=10, color='lightgreen', edgecolor='black')
plt.axvline(np.mean(crecimiento), color='blue', linestyle='dashed', linewidth=2)
plt.title(f"Histograma de Crecimiento de Plantas \n Asimetría = {asimetria:.2f}")
plt.xlabel("Altura (cm)")
plt.ylabel("Frecuencia")
plt.show()

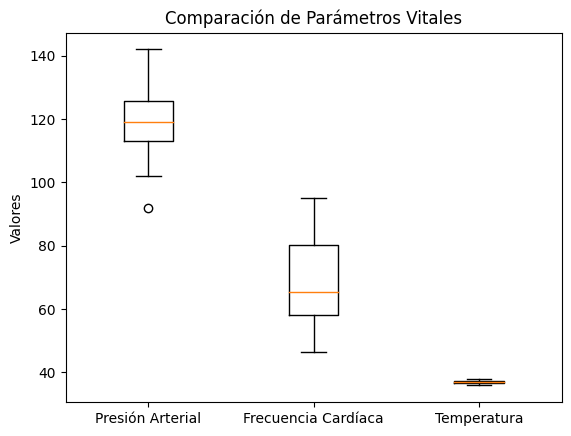
##Ejercicio 3: Coeficiente de variación - comparación de parámetros vitales En medicina, se comparan diferentes parámetros vitales de los pacientes (presión arterial, frecuencia cardíaca, temperatura corporal). El coeficiente de variación (CV) es una medida que permite comparar la variabilidad de diferentes conjuntos de datos de forma estandarizada, ya que toma en cuenta la media y la desviación estándar.

El CV se expresa como un porcentaje, y cuanto mayor sea, mayor será la variabilidad en comparación con la media.

Instrucciones:

1. Simula datos de tres parámetros vitales (presión arterial, frecuencia cardíaca y temperatura).

2. Calcula el coeficiente de variación para cada parámetro.

3. Grafica boxplots para comparar la variabilidad de los datos.

import numpy as np
import matplotlib.pyplot as plt

# Simulamos datos de parámetros vitales
presion_arterial = __.random.normal(120, 10, 50)  # Presión arterial en mmHg
frecuencia_cardiaca = np.____.normal(70, 15, 50)  # Frecuencia cardíaca en latidos por minuto
temperatura = np.random.____(37, 0.5, 50)  # Temperatura en °C

# Calculamos el coeficiente de variación (CV)
cv_presion = __.std(presion_arterial) / np.mean(presion_arterial) * 100
cv_frecuencia = np.___(frecuencia_cardiaca) / np.____(frecuencia_cardiaca) * ___
cv_temperatura = np.std(_______) / __.mean(temperatura) * 100

# Mostramos los resultados
print(f"Coeficiente de Variación de Presión Arterial: {cv_presion:.2f}%")
print(f"Coeficiente de Variación de Frecuencia Cardíaca: {_________:.2f}%")
print(f"Coeficiente de Variación de Temperatura: {cv_temperatura:.2f}%")

# Graficamos los boxplots para comparar la variabilidad
plt.boxplot([_________, frecuencia_cardiaca, temperatura], labels=['Presión Arterial', 'Frecuencia Cardíaca', 'Temperatura'])
plt.title("Comparación de Parámetros Vitales")
plt.ylabel("Valores")
plt._____

Coeficiente de Variación de Presión Arterial: 8.71%
Coeficiente de Variación de Frecuencia Cardíaca: 19.83%
Coeficiente de Variación de Temperatura: 1.13%

#Conclusión En este notebook hemos explorado conceptos clave de estadística descriptiva, como la curtosis, asimetría y el coeficiente de variación, y su aplicación en diversas áreas científicas. A través de ejemplos y visualizaciones gráficas, hemos visto cómo estas herramientas nos permiten analizar la forma y variabilidad de los datos, proporcionando una mejor comprensión de fenómenos del mundo real.

Este conocimiento permite aplicar técnicas estadísticas en sus proyectos y tomar decisiones más informadas basadas en los datos.